Szczepienia to jedno z największych osiągnięć interdyscyplinarnej nauki (nie tylko medycyny lecz także matematyki i w coraz większym stopniu również nauk społecznych). Opanowanie aktualnej pandemii COVID-19 zależy od wyciągnięcia wniosków z burzliwej historii szczepień. Co ciekawe, nie dość że pierwszy matematyczny model epidemiologiczny jaki kiedykolwiek powstał, opisywał dane dotyczące epidemii czarnej ospy w XVII wiecznym „naszym” Wrocławiu, to przede wszystkim głównym celem była analiza ryzyka i korzyści wariolizacji – czyli prekursora szczepień zastąpionych przez pierwszą szczepionkę w rozumieniu dzisiejszym na przełomie XVIII/XIX w. Tu po raz pierwszy historia zatoczyła koło, gdyż to właśnie we Wrocławiu w roku 1963 wybuchła ostatnia epidemia czarnej ospy w Polsce, krótko przed eradykacją choroby. To właśnie głównie dzięki szczepieniom prewencyjnym osób z ryzykiem kontaktu udało się tę epidemię opanować.
Prezentujący swoje wyniki dotyczące modelu wrocławskiego analizy korzyści i ryzyka “szczepień” w 1766 roku w Paryżu, jeden z największych matematyków w dziejach ludzkości ‐ Daniel Bernoulli, powiedział: „Po prostu wierzę, że w materii jakości życia ludzkiego, żadna decyzja nie zostanie podjęta, bez wszelkiej wiedzy, którą obliczenia i analizy mogą dostarczyć” (tłum. Jarynowski).
W tym czasie (w drugiej połowie XVIII wieku) rozwijana była procedura wprowadzania zakażenia przez skórę, aby wywołać łagodniejszą chorobę niż w przypadku zakażenia wirusem Variola Vera drogą oddechową, ale taką, która wywołuje odporność. Wariolizacja nie była pozbawiona ryzyka, a Bernoulli użył swojego modelu, aby porównać prawdopodobieństwo śmierci po “szczepieniu” (ryzyko) w porównaniu z zyskiem w długości życia wynikającym z uniknięcia pełnoobjawowej choroby (korzyść).
Należy podkreślić, że to właśnie wtedy ów epizod wrocławski zapoczątkował rozwój nowej nauki czyli epidemiologii, która dzięki matematyce i do której później dołączyła socjologia, mogła stać się wiodącą dziedziną medycyny w czasach nawracających epidemii.
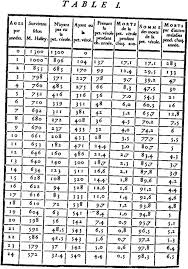
Bernoulli oparł się w swojej pracy na tabelach umieralności miasta Wrocław, gdzie wiek i płeć każdego zmarłego w danym miesiącu zostały zapisane i porównane z liczbą urodzin z pięciu lat (od 1687 do 1691), które to zostały przygotowane z zachowaniem wszystkich wymagań dokładności i szczerości. Po zastosowaniu wielu uproszczeń otrzymał średnią długość życia w stanie naturalnym jako EN 26 lat i 7 miesięcy, a dla sytuacji w której nie występowałaby ospa prawdziwa EV 29 lat i 9 miesięcy.
Po czym wyznaczył krytyczne prawdopodobieństwo zgonu z powodu wariolizacji (p=1-EN/EV~11%), poniżej którego korzyść ze “szczepienia” przewyższa ryzyko z tym związane dla populacji Wrocławia. Oczywiście, korzystając z bazowego modelu wrocławskiego przeliczył ów próg dla innym miast, np. Londynu czy Paryża, dla których tak dokładne dane nie były dostępne.
Warto podkreślić, że parametry wprowadzone i wyestymowane przez Bernoulliego dzięki tabelom wrocławskim są stosowane (czasami w identycznej formie, czasami z niewielkimi zmianami w postaci innych estymatorów) w epidemiologii do dziś: presja zakażenia/wirusa (prawdopodobieństwo zachorowania w danym roku), śmiertelność (IFR-infection fatality rate), odporność zbiorowiskowa (procent populacji udodpornionej powyżej którego epidemia się nie szerzy), itp.
Analizy Bernoulliego wywołały ogromną falę zainteresowania w europejskim środowisku naukowym (z czym również mieliśmy do czynienia w związku pandemią COVID-19). Z powodu braku danych wysokiej jakości, Bernoulli założył ryzyko zgonu z powodu wariolizacji na poziomie 1%, d’Alembert 2%, a Diderot 0.5%. Tak więc, temat szczepień i rozbieżności w szacowaniu i percepcji ryzyka zajmują elity intelektualne już od prawie 300 lat.
Też już XVIII-to wieczni filozofowie społeczni zidentyfikowali paradoksy percepcji ryzyka gdyż wariolizacja wiązała się z niebezpieczeństwem zgonu “tu i teraz”, a uniknięcie śmierci czy powikłań z powodu czarnej ospy odnosi się do abstrakcyjnej przyszłości. Już wtedy wyodrębniono dylemat ryzyka i korzyści pojedynczej jednostki oraz całego społeczeństwa (szczepiąc siebie jednostka podejmuje ryzyko indywidualne, ale korzyść może być również zbiorowa chroniąc inne osoby poprzez zmniejszenie presji wirusa w populacji).
Zastosowanie metod matematycznych i modelowania szczepień w epidemiologii jest już bardzo starym podejściem opisania i przewidywania zjawisk wpływających na populacje. Tym bardziej, że mniej więcej od wybuchu epidemii HIV (w czerwcu 2021 mija 40 lat) dysponujemy danymi z randomizowanych badań klinicznych oraz po-autoryzacyjnymi rejestrami, dzięki czemu modele korzystają z bardziej dokładnych danych i mogą znacznie więcej zmiennych uwzględniać. Z tym, że to teraz dane pozyskane z badań klinicznych i obserwacyjnych z innych ośrodków są wykorzystywane do budowy modeli dla Wrocławia, a my w Polsce praktycznie nie prowadzimy wysokiej jakości rejestrów ani niekomercyjnych badań klinicznych w zakresie chorób zakaźnych. Dodatkowo w dobie rozwoju technologii informatycznych wspomaganie procesów np. symulacje przez inteligentne systemy komputerowe wyposażone w bazy wiedzy dziedzinowej (o kontaktach społecznych, skuteczności szczepień, NOP-ach, itp.). Daje to możliwość stosowania i projektowania działań prewencyjnych (np. ustalanie optymalnej kolejności szczepień jak i precyzyjnej kalkulacji kosztów). Jednak już XVIII-to wieczni „modelarze” epidemii zauważyli, że największym problemem jest tak zwany “czynnik ludzki”, czyli szereg trudnych do przewidzenia reakcji społeczeństwa na zmieniające się bodźce.
Warto podkreślić, że Bernoulli zaproponował swoje statystyczne podejście porównujące korzyści i ryzyka płynące ze szczepień, z uwzględnieniem wieku i płci dzięki danym pochodzącym właśnie z Wrocławia. Tym bardziej musimy zrozumieć, że dyskurs jaki w chwili obecnej ma miejsce w związku ze szczepieniem p/COVID-19 coraz to młodszej populacji, nie jest niczym nowym. Zwłaszcza iż wiemy, że z malejącym wiekiem wzrasta ryzyko potencjalnych NOP-ów, a jednocześnie zmniejsza się korzyść indywidualna związana z uniknięciem zakażenia (czy jego ciężkiego przebiegu). Rolą lekarzy (i innych profesjonalistów medycznych) kwalifikujących do szczepień będzie znany już od wieków problem dokonania indywidualnej oceny korzyści i ryzyka w warunkach niepewnej informacji, ale również w wielu przypadkach jeszcze trudniejsze zadanie jakim jest przekonanie osoby lub opiekuna do wykonania szczepienia, gdy korzyści przewyższają ryzyka.
Literatura:
Bernoulli D, Essai d’une nouvelle analyse de la mortalité causée par la petite vérole et des avantages de l’inoculation pour le prévenir, Mem Math Phy Acad Roy Sci Paris, 1766.
Epstein S. Impure science: AIDS, activism, and the politics of knowledge. Univ of California Press; 1996.
Gigerenzer G, Edwards A. Simple tools for understanding risks: from innumeracy to insight. British Medical Journal, 2003, 327(7417), 741-744.
Jarynowski A. Obliczeniowe nauki społeczne w praktyce. WN:Głogów, 2014.
Jarynowski A, Grabowski A. Modelowanie epidemiologiczne dedykowane Polsce. Portal CZM. 2015;9(6).
Jarynowski A, Belik V, Choroby przenoszone drogą płciową w dobie Internetu i E-zdrowia–kalkulatory ryzyka, in Człowiek zalogowany, Kraków, Biblioteka Jagiellońska, 101-111, 2018;
Jarynowski A. Monitorowanie percepcji ryzyka Covid-19 na Dolnym Śląsku za pomocą analizy śladu cyfrowego w internecie 15.01-05.08. IBI:Wrocław, 2020.
Jarynowski A, Skawina I. Attempt at profiling and regionalisation of COVID-19 vaccine campaigns in Poland–preliminary results. Eur J Transl Clin Med. 2021;4(1):13-21.
Jarynowski A, Sputnik Vaccine Adverse Events (AEs) risk calculator, https://infodemia-koronawirusa.shinyapps.io/sputnik/, 2021.
MOCOOS, Zespół zajmujący się modelowaniem epidemii COVID-19 (m.in. dla Wrocławia i Dolnego Śląska), https://mocos.pl, 2020
Krueger T, Gogolewski K, Bodych M, Gambin A, Giordano G, Cuschieri S, Czypionka T, Perc M, Petelos E, Rosińska M, Szczurek E. Risk of COVID-19 epidemic resurgence with the introduction of vaccination passes. medRxiv. The Preprint Server for Health Sciences. 2021.
Seth C. Calculated Risks, Condorcet, Bernoulli, d’Alembert and Inoculation. MLN. 2014; 129(4):740-55.
* Ze specjalną dedykacją ku pamięci wielkiego popularyzatora matematyki prof. Wojciecha Okrasińskiego, który to zainspirował autora tekstu modelem Bernoulliego, w pierwszą rocznicę jego śmierci w czerwcu 2020.